Bertrand Ballot Theorem

The Bertrand Ballot Theorem gives the probability that in an election, where candidate A receives p votes and candidate B q votes with p > q, the probability that A will be strictly ahead of B throughout the count is (p-q)/(p+q).

Bertrand Ballot Theorem Calculator

Votes for candidate A
Votes for candidate B
Probability that A will be strictly ahead of B throughout the count	?

This can be used to see if you, or your investment manager, were skilful for just lucky. Suppose you have been ahead of a known index or benchmark every year for the last five years. The table below shows the yearly gain of a well known investment fund.

Fund Name	Year 1	Year 2	Year 3	Year 4	Year 5	Total Gain over 5 years
Invesco Perpetual Income Accumulation Units	26.59%	-8.58%	-20.85%	28.55%	8.54%	27.81%
Unit Trust Active Managed Funds Benchmark	7.17%	-3.26%	-23.32%	33.46%	5.87%	12.33%
Did Invesco beat the Benchmark	Yes	No	Yes	No	Yes	Yes, 3 years out of 5

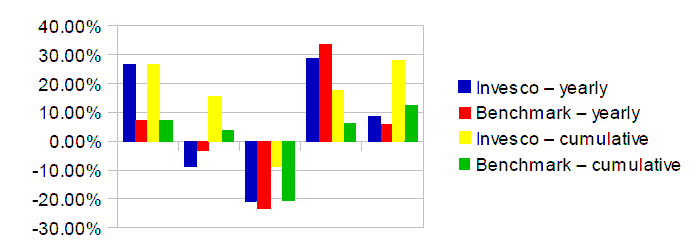
As can be seen from the graph below, Invesco (yellow bar) was always above the benchmark (green bar) at the end of each year even though it had some bad years.

This if often the way a performance graph is shown so that gains in the early years can mask poor performance in later years. In the box for "Votes for candidate A" put 3 - the number of years that Invesco beat the benchmark in that particular year. In the box for "Votes for candidate B" put 2 - the number of years that the benchmark beat Invesco in that particular year. This gives a result of 0.2 which means that there is a probability of 0.2 (20%) that given the final outcome (Invesco was ahead of the benchmark) it would have been expected that Invesco would be ahead of the benchmark in each of the 5 years.